今回紹介するのは、1971年に三省堂から発行された、遠山啓著先生著の

『楽しく読める気のきいた参考書 キュート数学Ⅱ』です。

タイトルの通り、本日は、“気のきいた”参考書をご紹介します。

どのような書籍であるのか、さっそくではありますが、はしがきに書かれた内容に注目していきましょう。

本書はふつうに教科書にはかかれていないような点に重点をおいてかかれている。諸君にとってつまずきの石となりそうなところは、対話体の特色を生かして、できるだけくわしく説明したので、教科書の足りない部分に対する補いとして役だつと思う。

教科書といえど、足りない部分、補いきれない部分というのが、やはりあるんですね。
実際学生時代、教科書さえしっかり読み込んでいれば理解できる、と思っていましたが、
なぜか理解できなくてつまづくポイントがたくさんありました。

この「キュート数学Ⅱ」を読み終えた頃には、つまずいていた石ころを飛び越えることができているのか、とても楽しみです。

まずは、遠山啓先生のご紹介からスタート！

遠山啓(とおやまひらく)

1909年熊本県生まれの数学者。
1938年東北大学理学部 数学科卒業。
海軍航空隊の教授を経て、1949年東京工業大学教授となる。

数学教育に非常に熱意を注がれており、その分野も小学生から一般の人まで、かなり幅広く、雑誌・新聞・単行本・学習書・教科書などで数学の啓蒙に活躍されている。

＝主な著書＝

「キュート数学Ⅰ」
「数学入門　上・下」
「無限と連続」
「現代数学対話」
「新数学勉強法」
「新数学Ⅰ」
「行列論」
「教師のための数学入門(数量編)」

まずは、本書がどのように構成されているのか見ていきます。

大きく第1章から第4章に分かれています。

第1章　分析と総合

ここでは、微分積分のありきたりな説明を飛ばして、いきなり計算問題に入っていきます。

第2章　収束と極限

ここでは、高校程度では避けがちな、ε(エプシロン)、δ(デルタ)を正面からとりあげて、徹底的に説明します。

第3章　微分

ここでは、その計算法と重要な関数のもとになる考え方を述べます。

第4章　積分

ここでは、微分にひき続いて基礎的な部分に力点をおきます。

それでは、内容を見ていきましょう。

本書のはしがきに、「対話体の特色を生かして・・・・」と書かれていたのを覚えていますか？

その言葉の通り、先生と理一君、文子さんの対話から数学の物語が始まっています。

洋裁の話をしたり、料理の話をしたりと、一見数学とはまったく関係のない話をしているようですが、すべては、微分と積分につながると、先生は言っています。

例えば、洋裁なら、布を切って縫い合わせていくわけですが、布を切ることは「分ける」にあたり、縫い合わせることは「つなぐ」にあたります。

少ししかつめらしいことばでいうと、「分ける」が「分析」、「つなぐ」が「総合」になります。

化学だって分析と総合が繰り返されており、例えば、プラスチックやポリエチレンという物質は、水とか石炭とかいう既存の物質を一度分けて
もう一度化合させたものなので、やはり分析と総合が利用されています。

人間の創造的活動は、「分けて、つなぐ」、つまり「分析し、しかるのちに総合する」ことだと言えます。

何が言いたいかというと、数学でも、この分析と総合が重要になってくるということです。

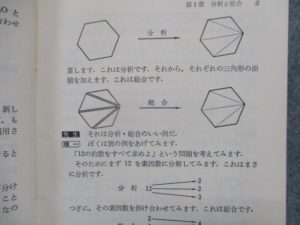
例えば、多角形の面積を計算するとき、一度三角形に分けて、それぞれの三角形の面積を計算し（←分析）、それから、それぞれの三角形の面積を加えます(総合)、よね。

このように、身近なものを例に挙げることによって、数学の本質を掴むことができるわけですね。

今のところ、＜数学の勉強＞をしているなーという感覚は一切ありませんね、とっても気楽に先生と会話を楽しんでいる雰囲気です。

さ、先に進めていきましょう。

ここでは、微分積分のおいたちについて触れられています。

ところで皆さんは、微分積分のおいたちについて今まで考えたことがありましたか？

恐らく、よほど数学が好きな人か、数学者を目指しているような人でない限り、
そんなことを考えることはないでしょう。

生まれた時には既に存在していたし、学校の授業で初めて耳にして、そこから当たり前のように授業が進んでいって、、、という感じでしたよね。

でも少し踏み込んでみると面白い発見がありそうです。

どんな時代に、どのようにして微分積分が生まれていったのか、数学をただの数字の羅列として認識するのではなく、
微分積分が生まれた背景を知ることで、自然と数学への興味がわき、勉強の意欲も沸いてくるかもしれません。

こんな内容は、普通、学校の教科書には載っていないですし、もちろん学校で習わないですよね。

本書は、参考書ではありますが、勉強をするぞ！という意気込みで挑む本ではなさそうですね。

あ、もちろん、参考書には違いないので、問題や解き方も掲載されています。

例えばこちら。

常に対話形式で話が進んでいくので、問題を解いている人が、どんな考えで、どのように解き進めているのか、どこでつまずいているのかがよくわかります。
また、合間合間に先生がヒントを与えてくれるので、勉強中に陥りがちな“孤独感”というものもありません。

ただただ問題を解いて、解答を確認して、という単純作業ではなく、常にディスカッションしながら生きた授業が受けられる、そんな印象です。

タイトル通り“楽しく読める気のきいた参考書”です。

わからなかったことがわかるってこんなに気持ちのいいものなのか、と実感させてくれる爽快な1冊です。

つまずきの石を蹴飛ばして、前進あるのみ！！