本日紹介するのは「ピタゴラスの定理100の証明法　幾何の散歩道」です。

著者は森下四郎先生です。

この書籍を見た瞬間に頭の中を流れたのは教育番組の「ピタゴラスイッチ♪」というワンフレーズでした。

正直番組自体は多く見たことはありませんが、カラクリ仕掛の装置や最後に流れるフレーズが頭の中でリピートしています。

教育番組では装置にピタゴラスの定理が使われているといったようなことではなく、「考える」ことに重点を置き身近に感じてもらいたいという思いのようです。

教育番組のホームページには

【4～6歳児を対象にした｢考え方｣を育てる番組】
-私たちがふだん何気なく暮らしている中には、さまざまな不思議な構造や面白い考え方、法則が隠れています。
番組では、毎回こうした面白い考え方や法則を取り上げ、それによって起こる事象を紹介し、「考え方」を育てることをねらっています。-

と掲載されていました。

確かに幼いうちから名前だけでも知っていたり、あれ？と気になるフレーズがあれば将来学習する時に興味を持ちやすかったり、こういう意味だったのか…と理解が早まるかもしれません。

勉強も仕事もいやいややるよりは楽しみながらの方が絶対にはかどりますからね。

本書の帯には「脳の筋トレ！書いて 描いて 引いて あなたにも、考えてほしい」と書かれています。

ウィキペディア（Wikipedia）によるピタゴラスの定理は

『初等幾何学におけるピタゴラスの定理（ピタゴラスのていり、英: Pythagorean theorem）は、直角三角形の3辺の長さの関係を表す。斜辺の長さを c, 他の2辺の長さを a, b とすると、定理はc 2 = a 2 + b 2 {\displaystyle c^{2}=a^{2}+b^{2}}

が成り立つという等式の形で述べられる[1][2][3]。三平方の定理（さんへいほうのていり）、勾股弦の定理（こうこげんのていり）とも呼ばれる。

ピタゴラスの定理によって、直角三角形をなす3辺の内、2辺の長さを知ることができれば、残りの1辺の長さを知ることができる。例えば、直交座標系において原点と任意の点を結ぶ線分の長さは、ピタゴラスの定理に従って、その点の座標成分を2乗したものの総和の平方根として表すことができる。このことは2次元の座標系に限らず、3次元の系やより大きな次元の系についても成り立つ。この事実から、ピタゴラスの定理を用いて任意の2点の間の距離を測ることができる。このようにして導入される距離はユークリッド距離と呼ばれる』

文章にしてみれば難しく感じられてしまいますが、本書のはしがきにもあるとおり、古くから数学のシンボルの1つとして取り扱われてきたもっとも有名な定理の1つです。

算数の授業でも学習した三平方の定理といわれると少し苦手意識が薄れるかもしれません。算数や数学を数式で考えるより、図形を使った問題の方が工作をしているような気持になれたので当時は楽しみながら問題を解いていたように思います。

本書の中で紹介されているピタゴラスの定理の証明は考え方にもよりますが約100です。

考えた人、考えた時代、逸話などを掲載することで理解しやすくなっていると思います。

書いて描いて引いてみれば、えんぴつ1本で脳力アップ。古今東西の「ピタゴラスの定理」証明法を集めて体系化。脳トレ問題満載。

そんな説明書きをされるくらい図形問題は考え方や見方を変える事で簡単に解けてしまったり、分かりやすい問題になる場合があります。その考える事こそが脳の筋トレになるのでしょう。証明方法が多い事がその理由かもしれません。

さて、本書の内容を一部紹介しましょう。

ピタゴラスの定理についての説明があり、証明法が紹介されています。

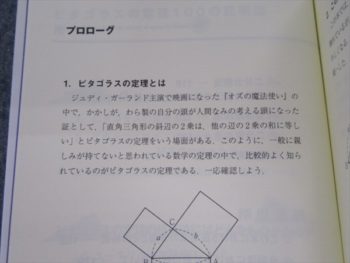
前述のとおり、証明を考えた人、考えた時代、逸話などが掲載されています。

証明方法を知るだけでなく、考えた人、考えた時代、逸話などを知ることによってより知識に深みが増すと思います。

より多くの問題を解く事で脳トレになるのはもちろんですが、自信につながることでしょう。

当サイトで紹介する書籍としては比較的手に取りやすい価格帯で販売されていますので、機会があればぜひ手にとってみてはいかがでしょうか？

それでは次回更新もお楽しみに。